Black-Oil Tables

whitson comment

Note from Markus Hays Nielsen: The notation used for associated surface volumes and rates (e.g. $V_{\bar{g}o}$) defines the surface volume type and from which reservoir phase it comes from - e.g. $V_{\bar{g}o}$ is the surface gas (denoted by $\bar{g}$) from the reservoir oil phase (denoted by $o$)).

The black-oil PVT model is a simplified fluid model using only two components (surface gas and oil) unlike the more complex compositional models like the cubic EOS models (e.g. Peng-Robinson and Soave-Redlich-Kwong). The properties that define the black-oil table are divided into the volumetric properties (i.e. the formation volume factors and surface volume ratios) and the viscosity for each phase. The volumetric properties are given by the oil and gas formation volume factors ($B_o$ and $B_g$) and the surface volume gas-oil ($R_s$) and/or oil-gas ratios ($r_s$ or $R_V$).

The main assumption of both the traditional and modified black-oil models are the following:

The surface densities are constant (i.e. $\rho_{\bar{g}g}=\rho_{\bar{g}o}$ and $\rho_{\bar{o}g}=\rho_{\bar{o}o}$ if the modified black-oil model is used)
The temperature is constant
Surface process is fixed and constant

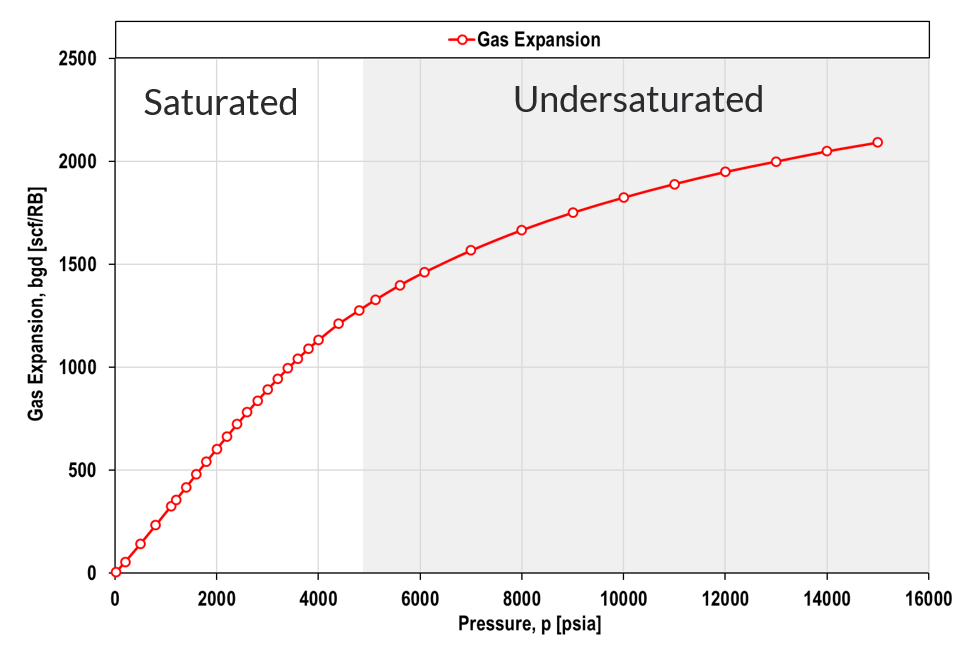
Black-oil tables are traditionally given in two parts; (1) a saturated points and (2) an undersaturated points. The saturated points are defined by a line on the black-oil property versus pressure plot where, at a given composition (or $R_s$) the pressure is equal to the saturation pressure. The second part of the black-oil table consists of undersaturated extensions where the composition is constant while the pressure increases beyond the saturation pressure.

whitson comment

Note from Markus Hays Nielsen: The reader is advised to think about why the solution GOR ($R_s$) or OGR ($r_s$) is used synonymously with the compositions for the black-oil model. This is a key concept that tests your knowledge of the black-oil model.

Historical Overview

Since the 1920's the petroleum industry has been aware of the need to describe how the volume of gas and oils relate with respect to pressure and temperature¹. Before the 1980's a so-called black-oil model was developed that described the relationship between the reservoir fluid volume(s) and the surface fluid volume(s). This traditional black-oil assumed that the oil reservoir volume would result in a surface gas and oil volume, while the reservoir gas volume simply expanded to a surface gas product.

In 1965 Kniazeff and Naville proposed a modified variation of the traditional black-oil model by including the retrograde condensation of oil from the reservoir gas volume². Although the modified model was introduced in the 1960's, it was not widely used in the industry until the 1980's.

In 2007 Singh et al. introduced a consistent approach to extending the black-oil tables while still maintaining physical constraints³. In this paper, examples of why extensions of the black-oil model are necessary was given and a set of physical constraints were also given. Recently, the whitsonᵖᵛᵗ software has developed a fully automatic approach to consistently extend the black-oil tables to either a critical mixture or a pressure bound if a critical mixture cannot be found.

Traditional Black-Oil Model

Early models for relating how the HC fluid volumes change with pressure were attempted as early as the 1920's. The traditional black-oil model was applied as the standard modeling method until the 1980's.

The traditional black-oil model assumes that from from a given reservoir volume of gas ($V_g$) there is an equivalent surface volume of gas from the reservoir gas phase ($V_{\bar{g}g}$), and given reservoir volume of gas ($V_g$) there is an equivalent surface volume of gas ($V_{\bar{g}o}$) and surface volume of oil ($V_{\bar{o}o}$) from the reservoir oil phase. With the two reservoir volumes (only one for single phase reservoirs) and the three associated surface volumes (only one or two for single phase gas or oil reservoirs), the following volumetric properties can be defined

$\begin{equation}\label{Bo_traditional} B_o(p) = \frac{V_o(p)}{V_{\bar{o}o}} \end{equation}$

$\begin{equation}\label{Bg_traditional} B_g(p) = \frac{V_g(p)}{V_{\bar{g}g}} \end{equation}$

$\begin{equation}\label{Rs_traditional} R_s(p) = \frac{V_{\bar{g}o}}{V_{\bar{o}o}} \end{equation}$

Modified Black-Oil Model

In the 1980's more complex hydrocarbon reservoirs became commercially conventional (e.g. gas condensates and wet gas fields) such that a modification to the traditional black-oil model became required.

The modified black-oil model is similar to the traditional black-oil model, but with the with a key difference in that the modified black-oil model accounts for liquid condensation from the reservoir gas phase ($V_{\bar{o}g}$). The addition of the condensate liquid volume from the gas phase introduces a fourth volumetric term, the oil-gas ratio (OGR), defined by

$\begin{equation}\label{rs_mod} r_s(p) = \frac{V_{\bar{o}g}}{V_{\bar{g}g}} \end{equation}$

The modified black-oil model also introduces a more accurate model for the gas FVF ($B_g$) as the true gas surface volume does not include the condensate that is removed from the reservoir gas. To distinguish between the "true" and "fake" gas FVF the terms dry and wet gas gas FVF are introduced using the nomenclature $B_{gd}$ and $B_{gw}$ respectively. The dry and wet gas FVF are only equal for dry reservoir gases where the condensate volumes are negligible.

Alternate Formulation of the Black-Oil Model

An alternate formulation can be used if molar amounts are used together with surface densities and molecular weights. The formation volume factor for oil and wet gas are given by

$\begin{equation}\label{Bo_alt} B_o(p) = \frac{n_{o}\frac{MW_o}{\rho_o}}{n_{\bar{o}o}\frac{MW_{\bar{o}}}{\rho_{\bar{o}}}} \end{equation}$

$\begin{equation}\label{Bgw_alt} B_{gw}(p) = \frac{p_{sc}}{T_{sc}}\frac{T}{p}Z(p) \end{equation}$

where $\bar{o}$ represents the surface oil and $o$ represents the reservoir oil.

The solution gas-oil ratio is given by

$\begin{equation}\label{Rs_alt} R_s(p) = \frac{n_{\bar{g}o}RT_{sc}/p_{sc}}{n_{\bar{o}o}MW_{\bar{o}}/\rho_{\bar{o}}} \end{equation}$

and similarly for the modified black-oil model, the oil-gas ratio is given by

$\begin{equation}\label{rs_alt} r_s(p) = \frac{n_{\bar{o}g}MW_{\bar{o}}/\rho_{\bar{o}}}{n_{\bar{g}g}RT_{sc}/p_{sc}} \end{equation}$

Extrapolation of the Black-Oil Tables

Note

The main article on black-oil table extrapolation is: Extensions of the Black-Oil Table

In 2007 Singh et al. published an approach to extrapolating the black-oil model past the original saturation pressure in a consistent manner³. Recently, as part of the whitsonᵖᵛᵗ software solution, a fully automated approach for generating black-oil extensions.

The main reason for extending the black-oil tables above the initial saturation pressure was sumarized by Singh et al . and is summarized here.

Consistency Check for Black-Oil Modeling

The set of three black-oil consistency checks defined by Sigh et al. are summarized here and is used to check that the existing or extended black-oil table abides by three physical restriction; (1) basic physcial restrictions of oils and gases, (2) critical point equality for oils and gases and (3) physical compressibility constraints.

Viscosity Models

whitson comment

Note from Bilal Younus: When choosing a viscosity model, the CSP model accurately predicts the oil and gas viscosities, but the LBC model can reproduce the same results as the CSP model after tuning and has the advantage of being faster to run. It is therefore recommended that, if data is available, to tune the LBC model to the data and if not, the LBC model can be tuned to CSP predicted data as using the LBC model will lead to faster run-times (e.g. in reservoir simulations).

Part of the black-oil tables is the reservoir gas and oil viscosities. These viscosities are either interpolated from some pre-made table, but more often the viscosities are defined by some viscosity correlation. These correlations range from simple models, like the Lee correlation, to intermediate models, like the Lohrenz-Bray-Clark (LBC) correlation, to more complex models, like the corresponding states principle (CSP) correlation.

Example Black-Oil Plots

GOR and OGR

Figure 1: Example of GOR for saturated and undersaturated region for a single composition.

Figure 2: Example of OGR (also called CGR for condensate-gas ratio) for saturated and undersaturated region for a single composition.

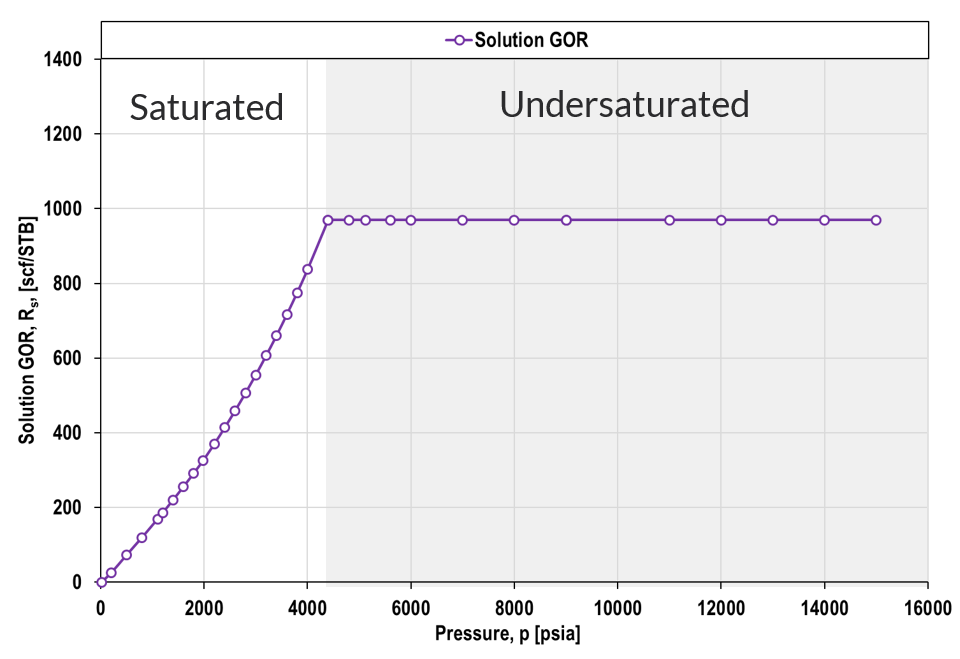
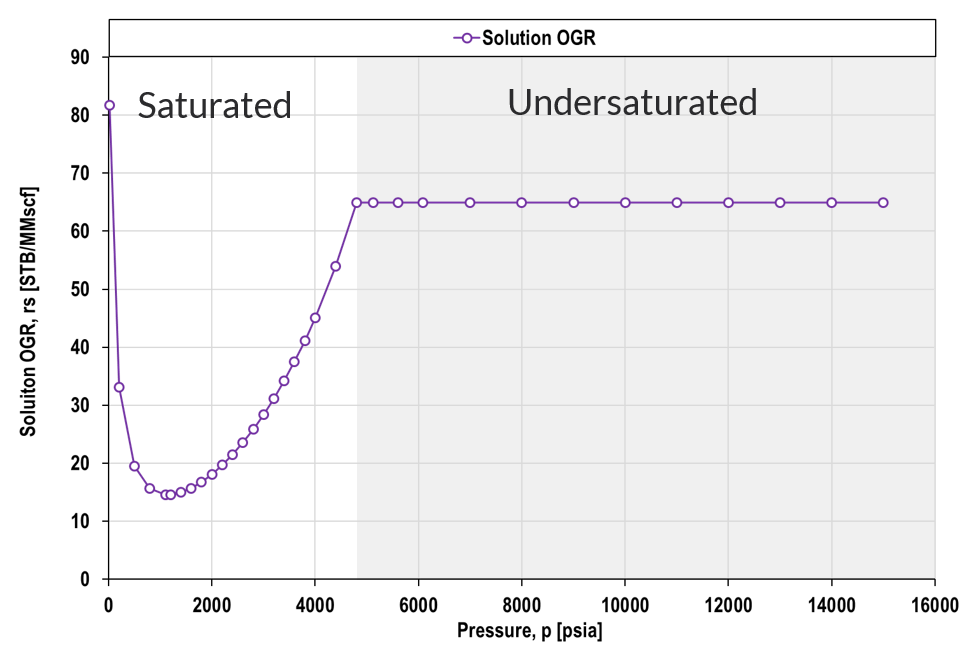
Formation Volume Factors

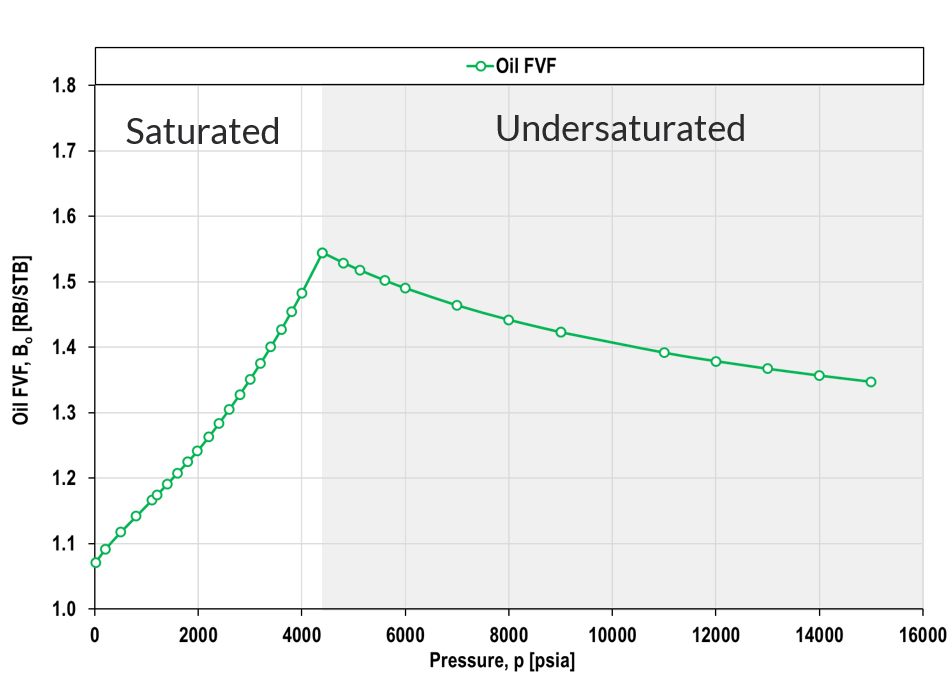
Figure of the oil formation volume factor FVF Bo

Figure 3: Example of oil FVF for saturated and undersaturated region for a single composition.

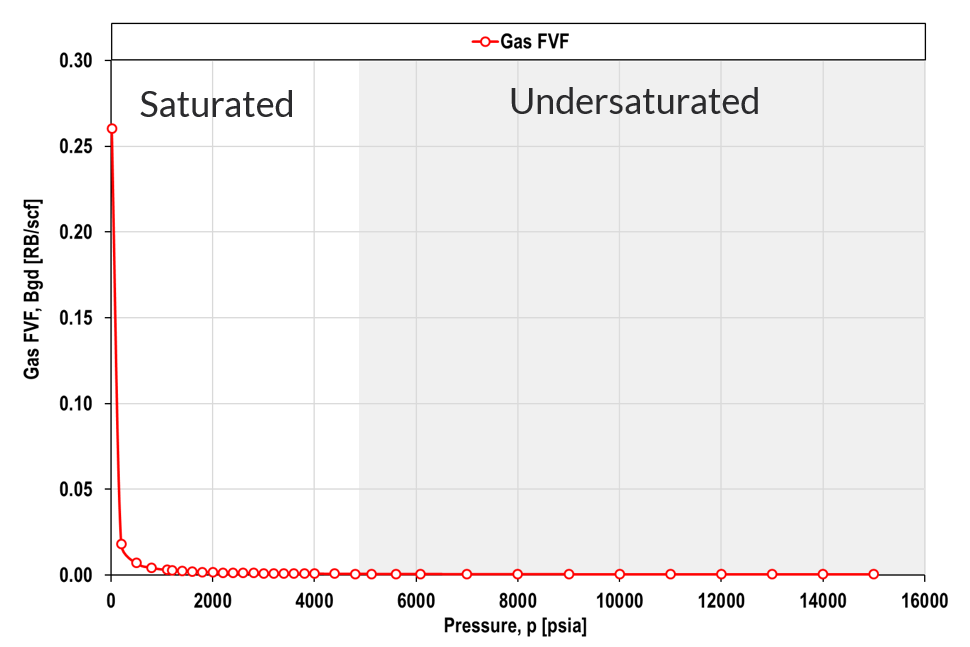
Figure of the gas formation volume factor FVF Bg

Figure 4: Example of gas FVF for saturated and undersaturated region for a single composition.

Figure of the gas expansion factor FVF 1/Bg

Figure 5: Example of gas expansion factor ($b_g=1/B_g$) for saturated and undersaturated region for a single composition.

Derivation of Oil and Gas Density Functions

Given the modified black-oil volumetric properties and the surface oil and gas densities it is possible to calculate the reservoir oil and gas densities.

Note

The derivation below is only for the reservoir oil density, but the same procedure can be done for the reservoir gas density by simply using the gas FVF and the oil-gas ratio instead of the oil FVF and the gas-oil ratio.

Starting with the definition of the oil FVF and applying the definition of density yields

$\begin{equation}\label{step_0} B_o = \frac{m_o}{m_{\bar{o}o}}\frac{\rho_{\bar{o}}}{\rho_o} \end{equation}$

Using the mass balance yields

$\begin{equation}\label{step_1} \frac{m_{o}}{m_{\bar{o}o}} = \frac{m_{\bar{o}o}+m_{\bar{g}o}}{m_{\bar{o}o}} \end{equation}$

Separating the fraction yields

$\begin{equation}\label{step_2} \frac{m_{o}}{m_{\bar{o}o}} = 1 + \frac{m_{\bar{g}o}}{m_{\bar{o}o}} \end{equation}$

Using the definition of the gas-oil ratio and applying the definition of density yields

$\begin{equation}\label{step_3} R_s = \frac{m_{\bar{g}o}}{m_{\bar{o}o}}\frac{\rho_{\bar{o}}}{\rho_{\bar{g}}} \end{equation}$

Re-arranging the equation \eqref{step_3} to isolate $\frac{m_{\bar{g}o}}{m_{\bar{o}o}}$ yields

$\begin{equation}\label{step_4} \frac{m_{\bar{g}o}}{m_{\bar{o}o}} = R_s \frac{\rho_{\bar{g}}}{\rho_{\bar{o}}} \end{equation}$

By inserting equation \eqref{step_4} into equation \eqref{step_2} yields

$\begin{equation}\label{step_5} \frac{m_{o}}{m_{\bar{o}o}} = 1 + R_s \frac{\rho_{\bar{g}}}{\rho_{\bar{o}}} \end{equation}$

By re-arranging equation \eqref{step_0} to isolate the reservoir oil density yields

$\begin{equation}\label{step_6} \rho_o = \frac{m_o}{m_{\bar{o}o}}\frac{\rho_{\bar{o}}}{B_o} \end{equation}$

and by inserting equation \eqref{step_5} into equation \eqref{step_6} yields the final result for the reservoir oil density

$\begin{equation}\label{step_final} \rho_o = \frac{\rho_{\bar{o}}+R_s\rho_{\bar{g}}}{B_o} \end{equation}$

Similarly, the reservoir gas density can be derived to be

$\begin{equation}\label{step_final_gas} \rho_g = \frac{\rho_{\bar{g}}+r_s\rho_{\bar{o}}}{B_{gd}} \end{equation}$

For reservoir water densities one of the following approaches can be used to derive pressure dependency of the density

Assume isothermal compressibility (no gas in solution - i.e. blue gas)
- Solve the differential equation to yield an exponential solution
- Simplify the exponential solution by using Taylor extrapolations (SENSOR approach).
Introduce blue-gas model to determine saturated water FVF

The approximate dry water solution proposed in the manual to SENSOR reservoir simulator is given by

$\begin{equation}\label{water_FVF} B_w = 1 - c_w \cdot (p_R-p_{sc}) \end{equation}$

with a reservoir water density given by

$\begin{equation}\label{water_dens} \rho(p_R) = [1-c_w\cdot(p_R-p_{sc})]\cdot \rho_{\bar{w}} \end{equation}$

C.S. Cragoe. Thermodynamic properties of petroleum products. Bureau of Standards, US Department of Commerce, pages 22, 1929. ↩
V. J. Kniazeff and S. A. Naville. Two-phase flow of volatile hydrocarbons. Society of Petroleum Engineers Journal, 5:paper SPE–962–PA, 1965. doi:https://doi.org/10.2118/962-PA. ↩
K. Singh, Oi. Fevang, and C. H. Whitson. Consistent black-oil pvt table modification. In SPE Annual Technical Conference and Exhibition, paper SPE–109596–MS. Society of Petroleum Engineers, 2007. doi:https://doi.org/10.2118/109596-MS. ↩↩