Real Gas Law
The real gas law is a simplification of the generalized equation of state (EOS) Z-factor definition. The simplification comes from the model only describing non-ideal gases and not multi-phase fluid systems. The real gas law takes a similar form as the ideal gas law and is defined by
where \(v\) is the molar volume (\(v=V/n\)) and \(Z\) is the simplified Z-factor which, in the case of the real gas law, can be described as the gas deviation factor.
Historical Overview
Early attempts to generalize the gas correction factor was made by Standing and Katz in 19441 by measurements of various petroleum gases and defining the now famous Stanging-Katz charts. By introducing pseudo-reduced variables for the pressure and temperature, they were able to generalize the behavior for a wide range of non-ideal pressures and temperatures. With increasing computer power becoming available, function based descriptions of the Standing-Katz charts became more applicable like the original and modified Benedict-Webb-Rubin (BWR) EOS models2. Other well known descriptions of the gas deviation factor like the Hall-Yarborough model3 are also applied to describe real gases. Modern descriptions of petroleum fluids are typically calculated using cubic EOS models like the Peng-Robinson or Soave-Redlich-Kwong EOS models.
Standing-Katz Z-Factor Charts
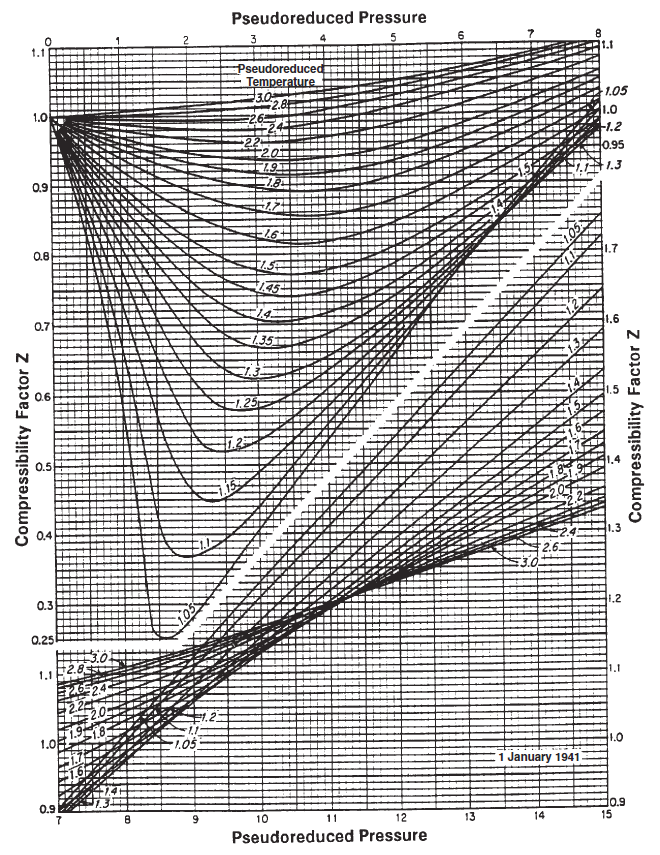
Figure 1: Standing-Katz chart.
The Standing-Katz chart is a best fit model for the Z-factor of various petroleum gases as a function of the specific gas reduced properties. The approach for finding the gas deviation factor is described by:
- Estimate the pseudo-reduced pressure and temperature by correlation (if no composition is given) or by Kay's mixing rule (if compositions are given).
- Locate the pseud-reduced pressure on the x-axis and then move along the y-axis until you cross the correct pseudo-reduced temperature iso-line.
- Move along the x-axis relative to the point found in step 2 to the left (if the pseudo-pressure is less than 7) or right (if the pseudo-pressure is greater than 7) to find the estimate of the Z-factor.
Hall-Yarborough Estimation of Gas Z-factor
The Hall-Yarborough approach to estimating the gas Z-factor is an iterative approach using the pseudo reduced properties of the gas (\(p_{pr}=p/p_{pc}\) and \(T_{pr}=T/T_{pc}\)) and the Carnahan-Standing hard-sphere EOS given by
where
and
The reduced density parameter (\(\hat{\rho}\)) is defend by solving
where
and the derivative is given by
where
The procedure for the Hall-Yarborough Z-factor is given below and more details about the procedure can be found in the SPE Monograph Phase Behavior4:
- Guess reduced-density parameter (\(\hat{\rho}\))
- Calculate objective function (\(f(\hat{\rho})\)) and its derivative (\(f'(\hat{\rho})\))
- Check if objective function is less than the tolerance (\(f(\hat{\rho})<\epsilon\))
- If the objective function is less than the threshold then the reduced-density parameter is correct and the user should move on to step 5. If the objective function is not less than the threshold then the reduced density parameter must be updated by Newton's method and the used must return to step 2.
- With the converged reduced-density parameter, calculate the Z-factor from the Carnahan-Standing had-spere EOS equation \eqref{eq:CS_eos}.
Estimates for Pseudo-Critical Properties
Note
All the correlation below are using absolute temperatures in Rankine (\(^\circ\)R) and absolute pressures in psia.
There are several methods for estimating the pseudo-critical properties of a gas. The first approach is by correlation. This approach is typically used if there is no available composition or component properties (\(p_c\), \(T_c\) or \(MW\)). Below there are two correlations given for estimating the pseudo-critical properties. The second approach to estimating the pseudo-critical properties is by applying Kay's mixing rule.
Sutton Correlation for Pseudo-Critical Properties
whitson comment
From Curtis Hays Whitson: We have found that using the Sutton correlation yields better results than Kay's mixing rule.
where \(\gamma_g\) is the gas specific gravity (\(\gamma=\rho/\rho_{ref}\)).5
Standing Correlation for Pseudo-Critical Properties
For dry gases where \(\gamma_g < 0.75\) the pseudo-critical properties can be estimated from
For wet gases where \(\gamma_g >= 0.75\) the pseudo-critical properties can be estimated from
where \(\gamma_g\) is the gas specific gravity (\(\gamma=\rho/\rho_{ref}\)).6
Kay's Mixing Rule for Pseudo-Critical Properties
Note
See article on PVT propertis for more details and example values for the molecular weights and critical properties.
Given a mixture \(y_i\) containing a gas composition where the molecular weight and critical properties are known for each component. With this information the pseudo-critical properties can be calculated from
-
M.B. Standing and D.L. Katz. Vapor-liquid equilibria of natural gas-crude oil systems. Transactions of the AIME, 155:paper SPE–944232–G, 1944. ↩
-
M. Benedict, G. B. Webb, and L. C. Rubin. An empirical equation for thermodynamic properties of light hydrocarbons and their mixtures i. methane, ethane, propane and n-butane. The Journal of Chemical Physics, 8:334–345, 1940. doi:https://doi.org/10.1063/1.1750658. ↩
-
K. R. Hall and L. Yarborough. A new equation of state for z-factor calculations. Oil Gas J, 71:82, 1973. ↩
-
C. H. Whitson and M. R. Brulé. Phase behavior. Volume 20. Henry L. Doherty Memorial Fund of AIME, Society of Petroleum Engineers …, 2000. ↩
-
R.P. Sutton. Compressibility factors for high-molecular-weight reservoir gases. In SPE Annual Technical Conference and Exhibition, paper SPE–14265–MS. Society of Petroleum Engineers, 1985. doi:https://doi.org/10.2118/14265-MS. ↩
-
M.B. Standing. Volumetric and phase behavior of oil hydrocarbon system. Society of Petroleum Engineers of AIME, Dallas, 1981. ↩