Phase Envelope

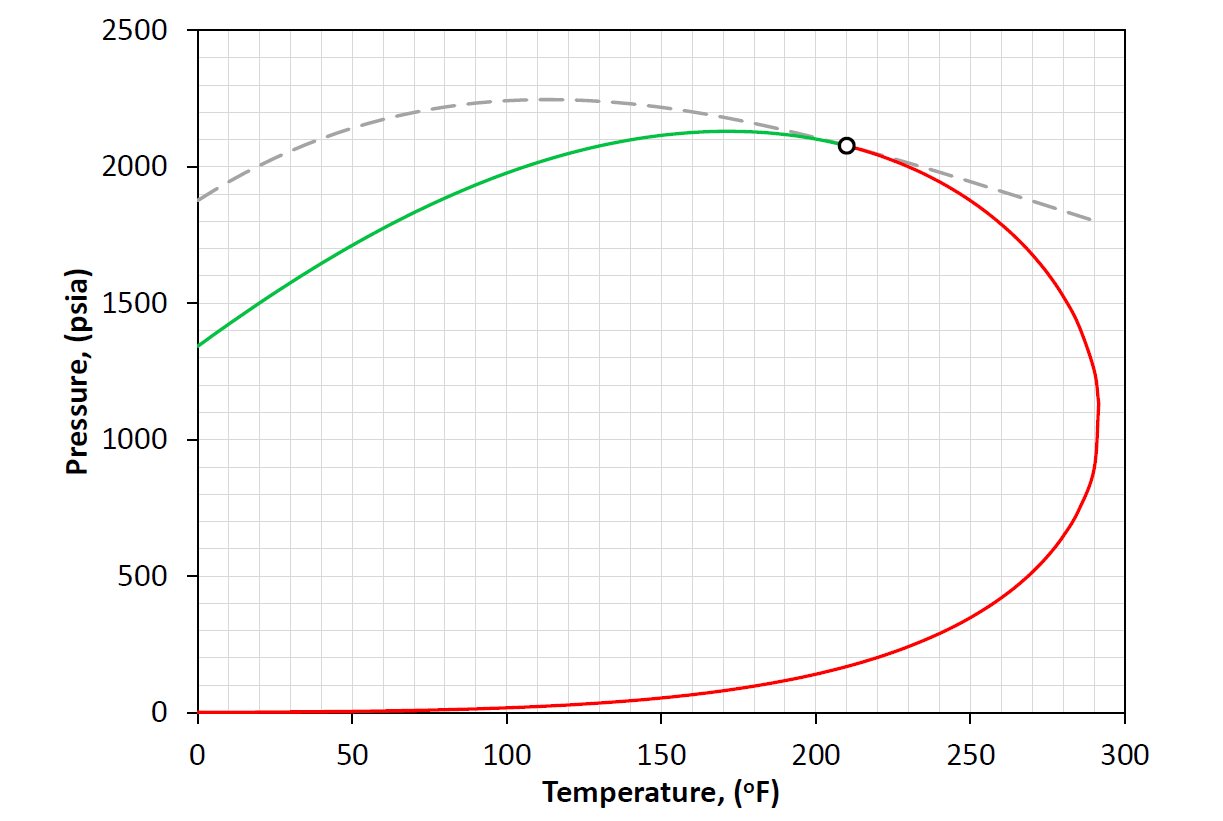
Figure 1: An example of a PT phase envelope (bubble point in green and dew point in red) and the convergence pressure as a function of temperature (grey dashed line).

Dew-Point Line

A dew-point is a phase behavior property defined by the pressure where an infinitesimal droplet of liquid is released from a single phase vapor at a given temperature and composition.

An example is given in Figure 1 where the dew-point line is shown as a red line. Note that for most (if not all) hydrocarbon systems there are two set's of dew-point pressures (called the upper and lower dew-points) in the upper and lower half of the phase envelope.

Bubble-Point Line

A bubble-point is a phase behavior property defined by the pressure where an infinitesimal bubble of vapor is released from a single phase liquid at a given temperature and composition. An example is given in Figure 1 where the bubble-point line is shown as a green line.

Critical Point

The critical point is the saturation pressure where the dew-point and bubble-point curves meet at a point. There are several unique features of the critical point, namely that (1) the vapor and liquid properties converge to the same values and (2) that the vapor molar fraction becomes arbitrary between the range of 0 and 1.

An example is given in Figure 1 where the critical point is shown as a black circle.

Convergence Pressure

The pressure of a fluid mixture at a given temperature where the K-values of all components appear to converge to unity when the isothermal (\(\log (K_i) - \log (p)\)) curves are extrapolated to pressures above the upper saturation pressure (i.e., into the undersaturated pressure region).

The convergence pressure of a fluid mixture with composition zi is the critical pressure for a fictitious “convergence” composition (\(z_{ki}\)) with a critical tie line passing through \(z_{i}\). The convergence pressure can usually be calculated by an EOS model based on the negative flash calculation, where the two equilibrium phase amounts approach ∞ and 1-∞.

An example is given in Figure 1 where the convergence pressure curve is shown as a dashed grey line.

Vapor Pressure

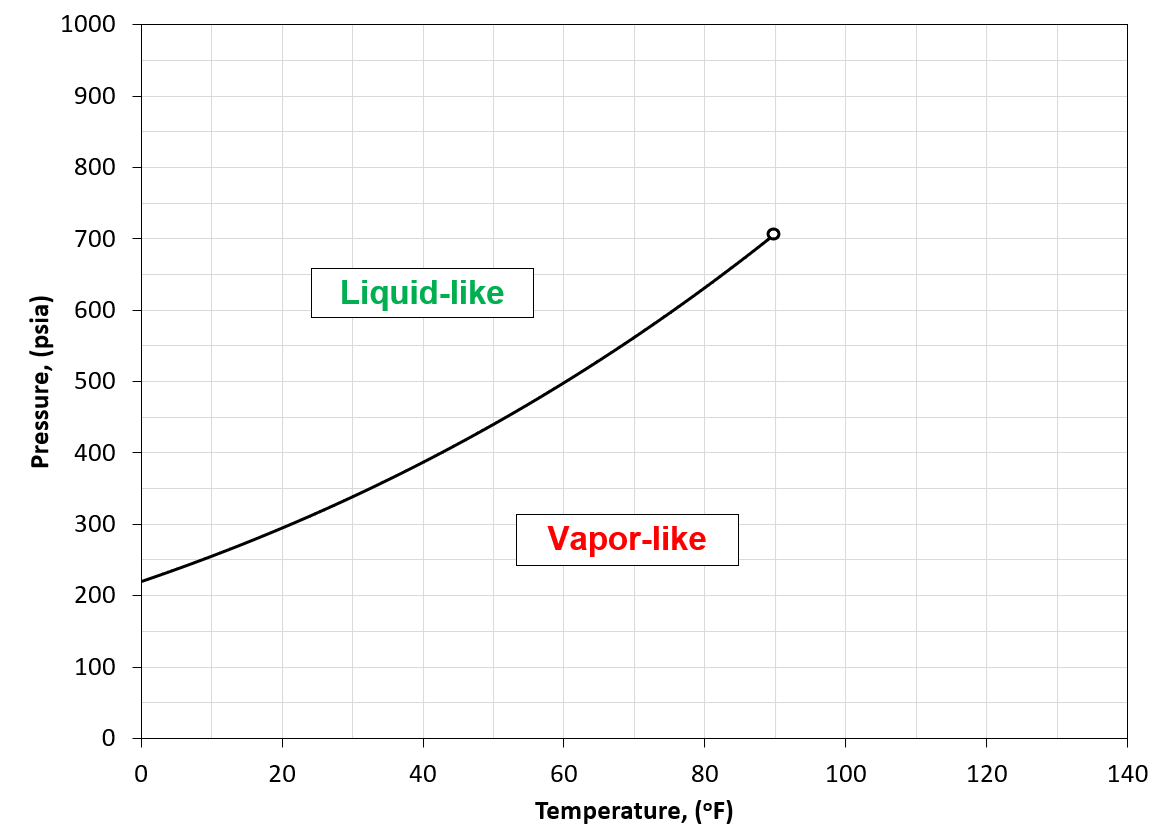
Figure 2: Vapor pressure line in the pressure-temperature plane for \(C_2\) (solid black line) and critical point for \(C_2\) (black circle).

The vapor pressure (\(p_v\)) is the equivalent to a PT phase envelope for a single component. The definition of the vapor pressure line is defined as the point where, starting at a single phase (either vapor-like or liquid-like), then an increase or decrease in either the pressure or temperature will lead to either a bubble of vapor or droplet of liquid being vaporized or condensed out of solution.

An example is given in Figure 2, where the vapor pressure curve is given for ethane (\(C_2\)). The term liquid-like and vapor-like reflect the ambiguous nature of defining a single-phase vapor or liquid. As an example, imagine a process that starts in the liquid-like region. If only the temperature is increased (i.e. an isobaric process) past the vapor pressure line, then the definition of the phase change is clear. However, imagine a process where (1) the pressure is increased past the critical pressure, then (2) the temperature is increased past the critical temperature, then (3) the pressure is decreased to the original pressure and finally (4) the temperature is decreased to a temperature past the vapor pressure line. In this process there will be no well defined approach to determine the phase transition from liquid-like to vapor-like.

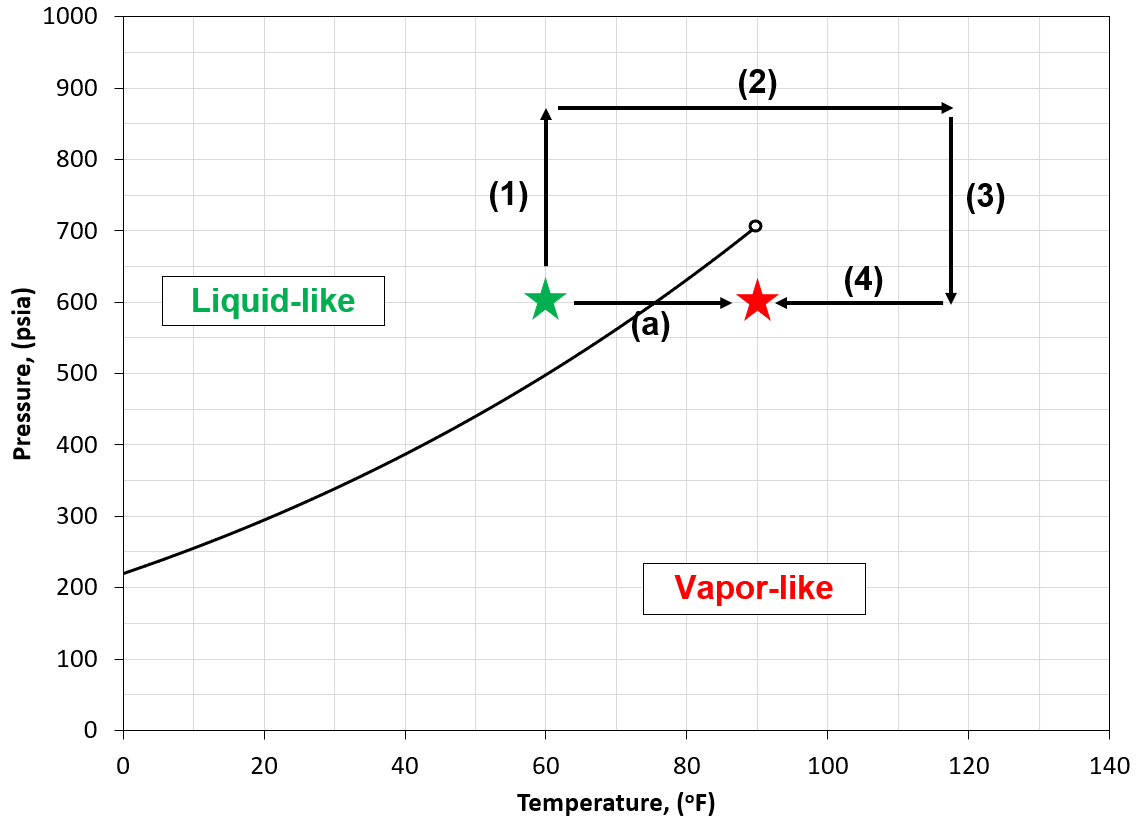
Figure 3: An example of the ambiguity related to single-phase labeling of fluids. Starting at a liquid-like state (green star) two paths (path (a) and path (1) through (4)) to the vapor-like (red star) shows that for path (1) through (4) there is no consistent method of defining the phase shift from "liquid" to "vapor" whereas path (a) goes through the vapor pressure curve where one can physically see the transition from "liquid" to "vapor".

Another example of the ambiguous nature of defining single phase fluids as "liquid" or "gas" by plotting the single phase density of pure propane is shown in Animation 1.

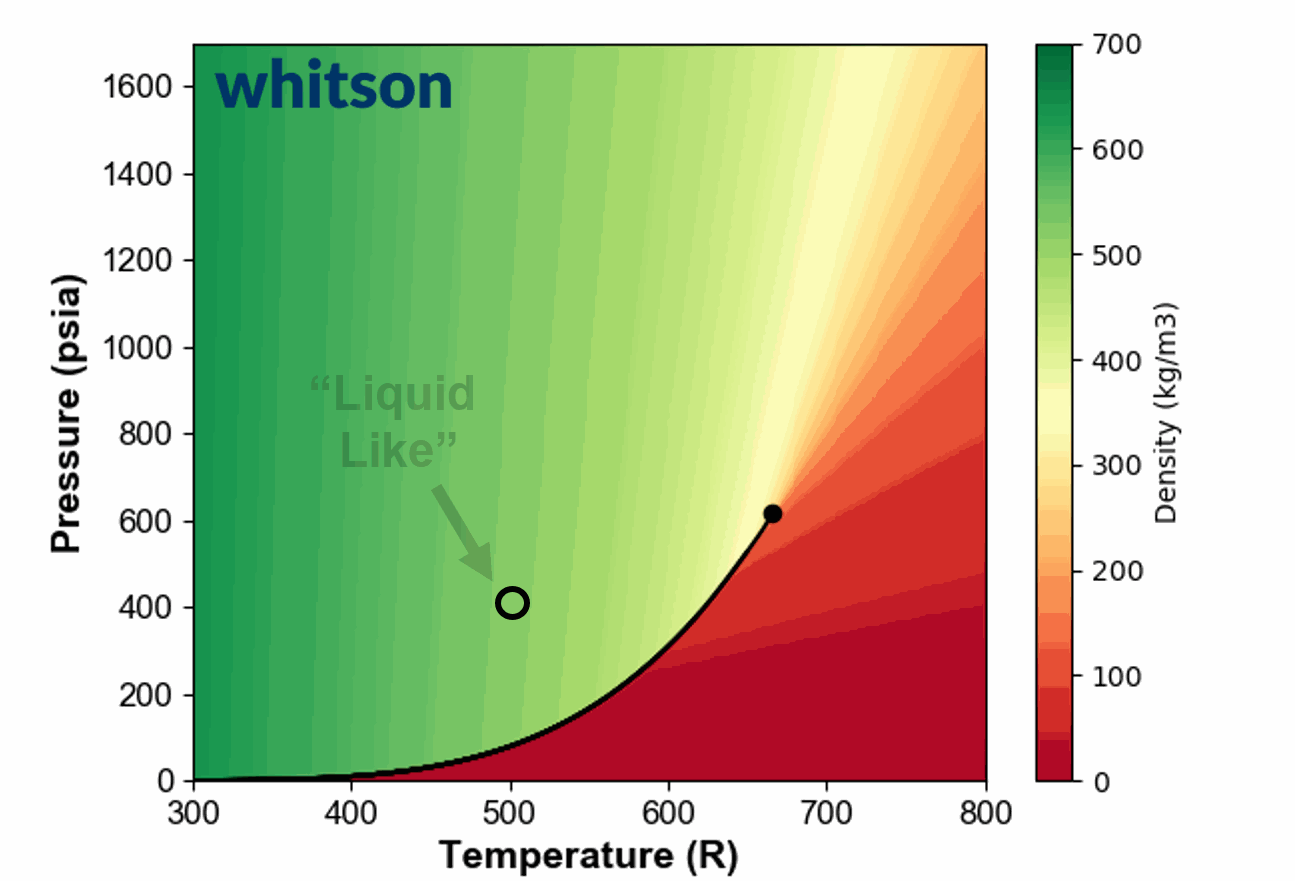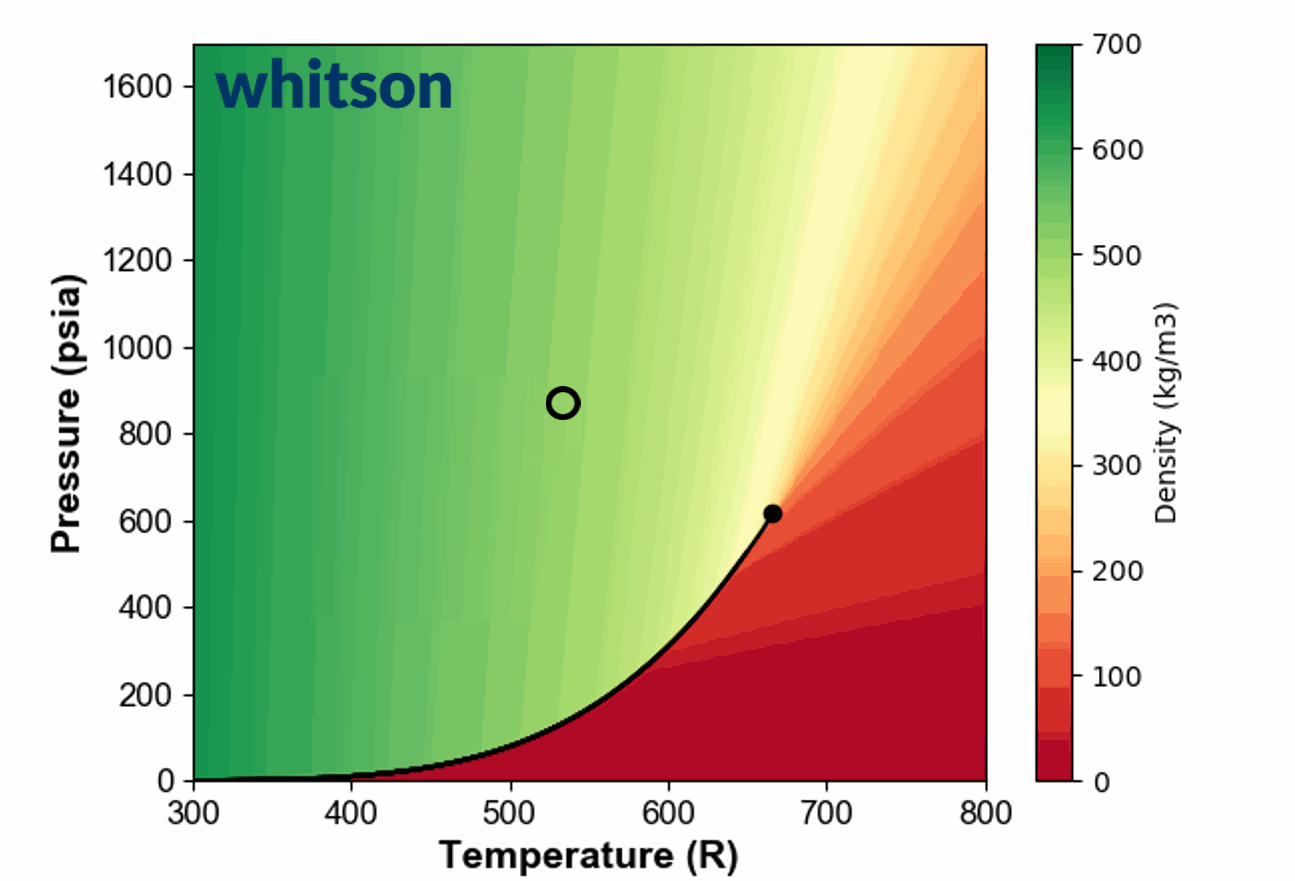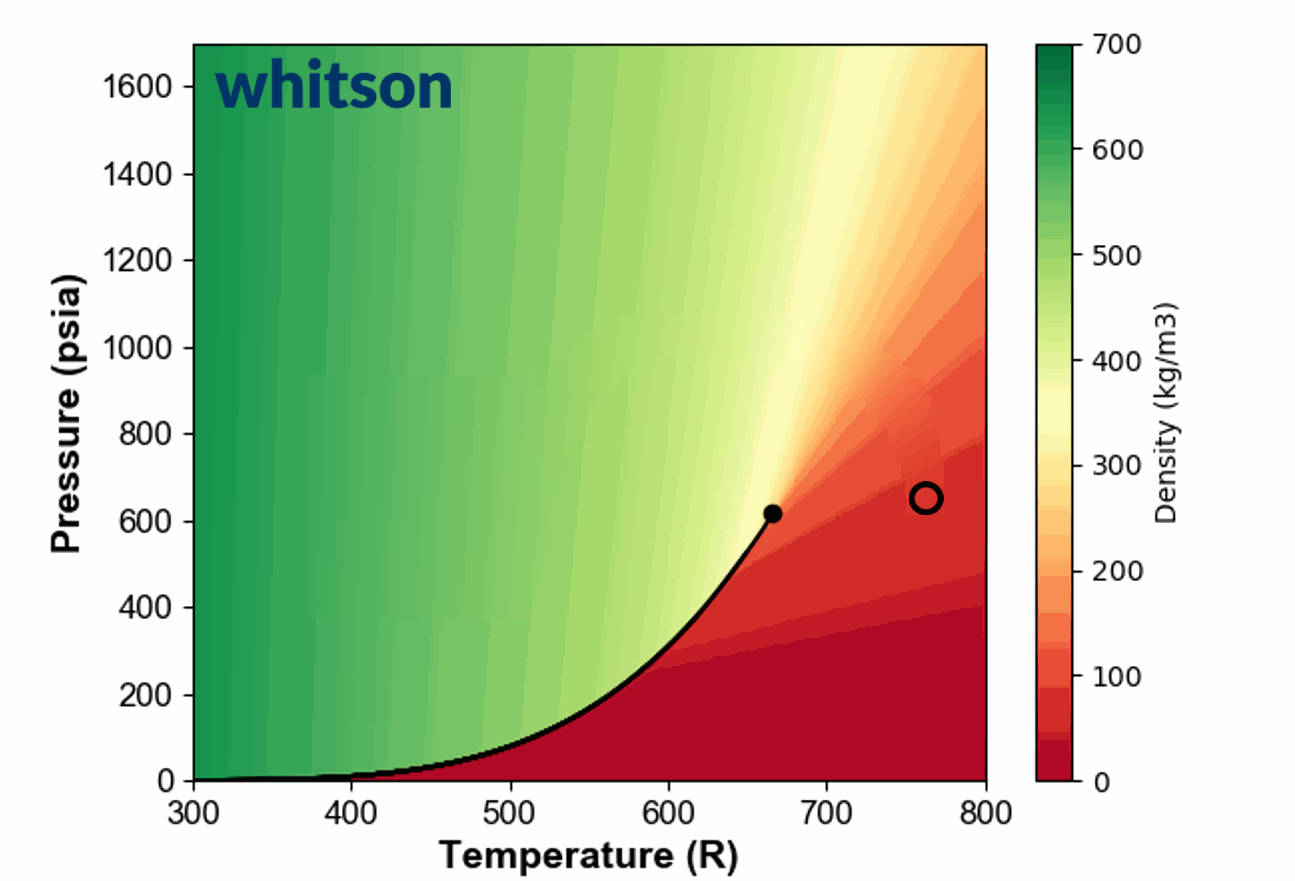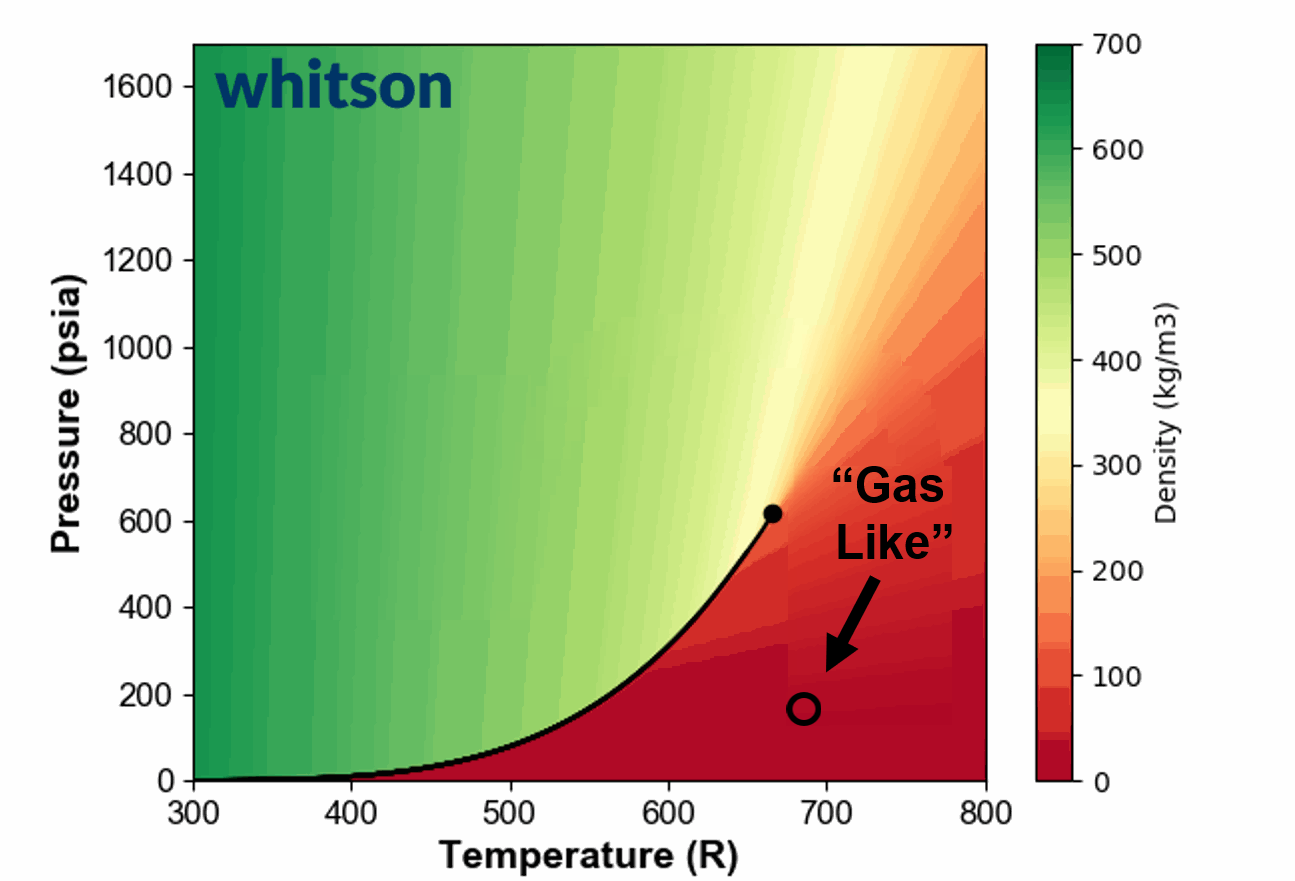
Animation 1: Animation showing the ambiguous nature of defining a single phase fluid a liquid or gas similar to the example in Figure 3. The contour colors are density for propane and the solid black line is the vapor pressure line for propane. The solid black circle is the critical point of propane.

An early method to estimate the vapor pressure is by the van der Waals algorithm using the equal area rule. Other methods have been proposed in the modern era and fall under the topic of computational thermodynamics.

Component Vapor Pressure

The component (or physical) vapor pressure line is defined for isomers or single components. In a multi-component system, the component vapor pressure curves act as a bound to the phase envelope of the mixture. An example is given in Figure 4 for a binary system containing \(C_2\) and \(C_5\) (left and right vapor pressure curves respectively) and a phase envelope containing a 50-50 mixture. As can be seen in Figure 4, the phase envelope is bounded by the vapor pressure curves of the binary components.

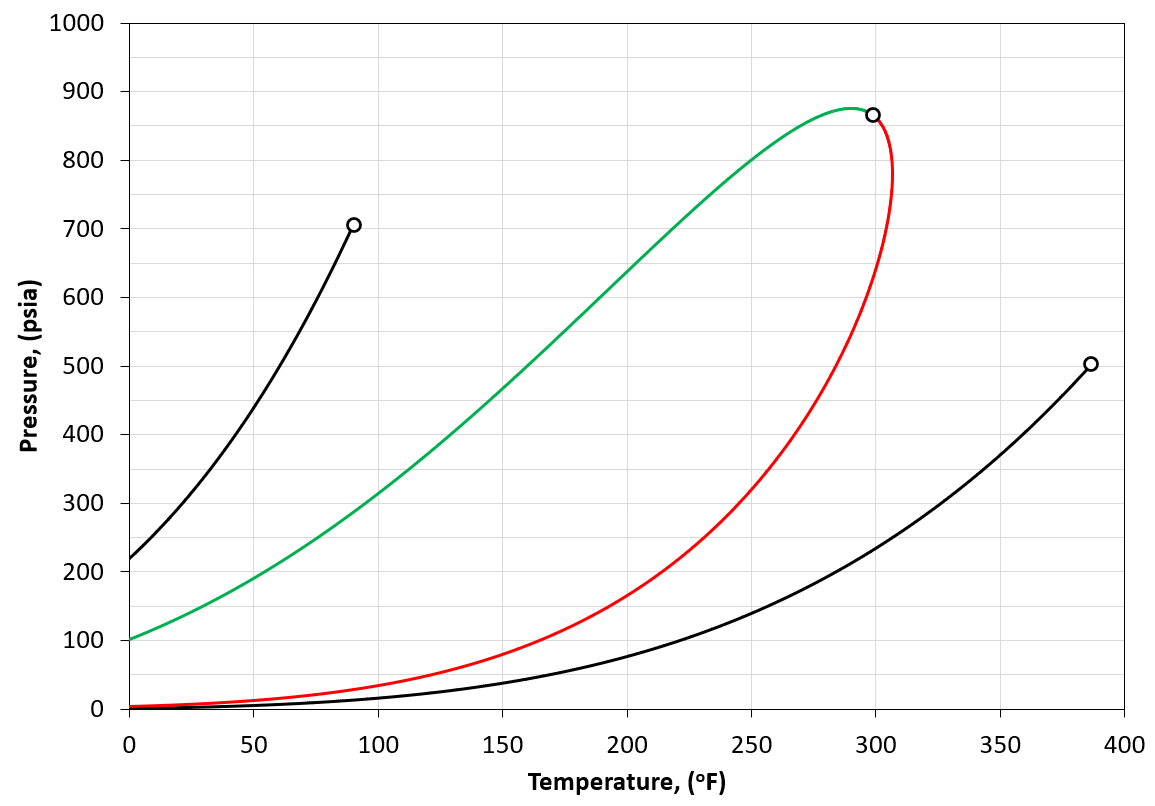
Figure 4: An example of a PT phase envelope (bubble point in green and dew point in red) of a 50-50 \(C_2\)- \(C_5\) binary system and the boundary composition vapor pressure lines (black solid line) for \(C_2\) and \(C_5\).

An animation of Figure 4 is given below.

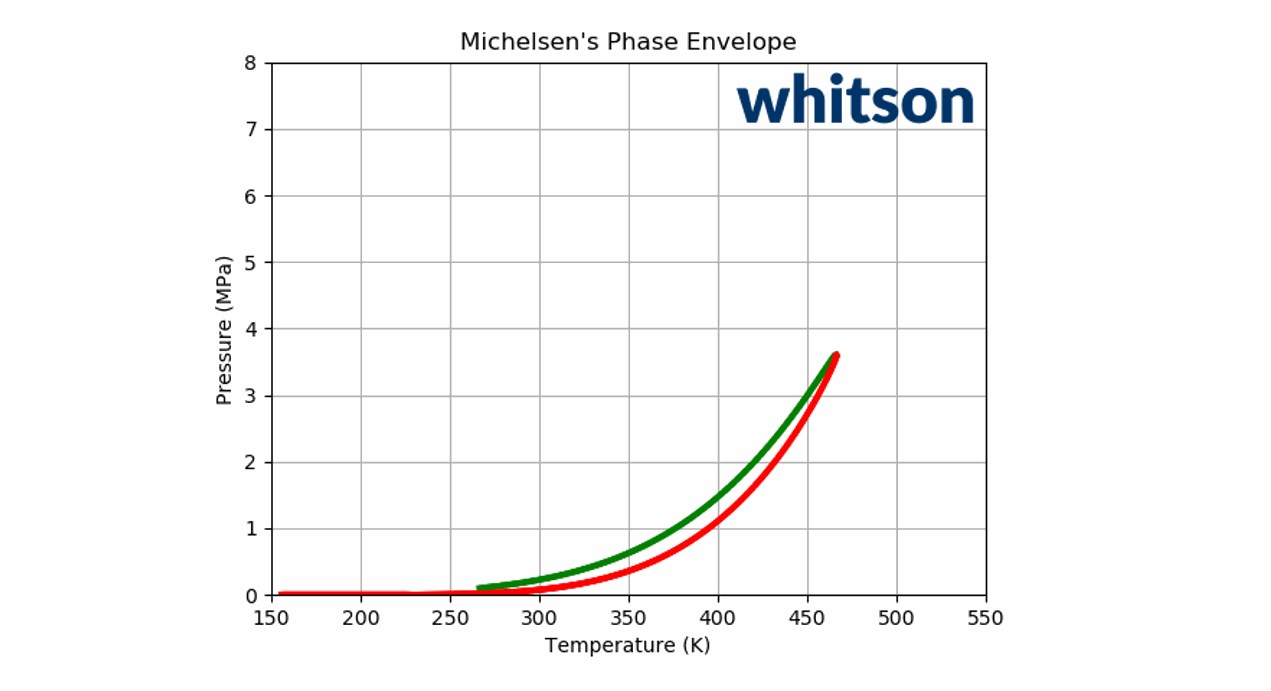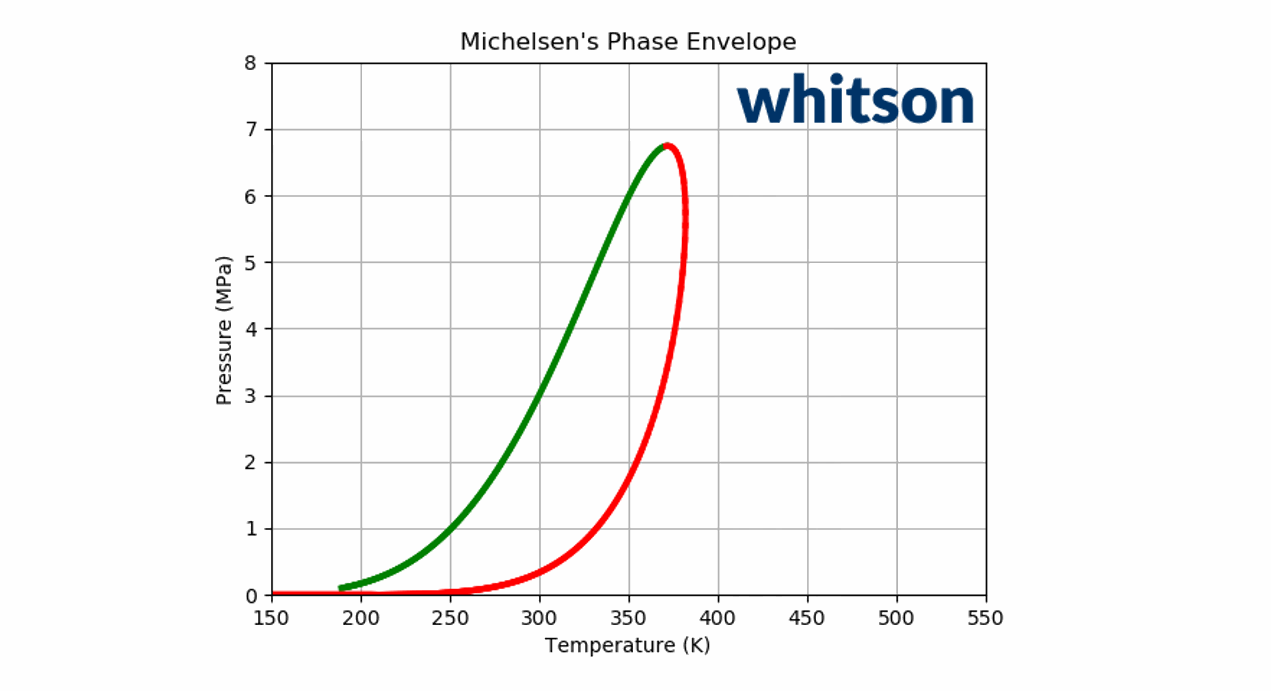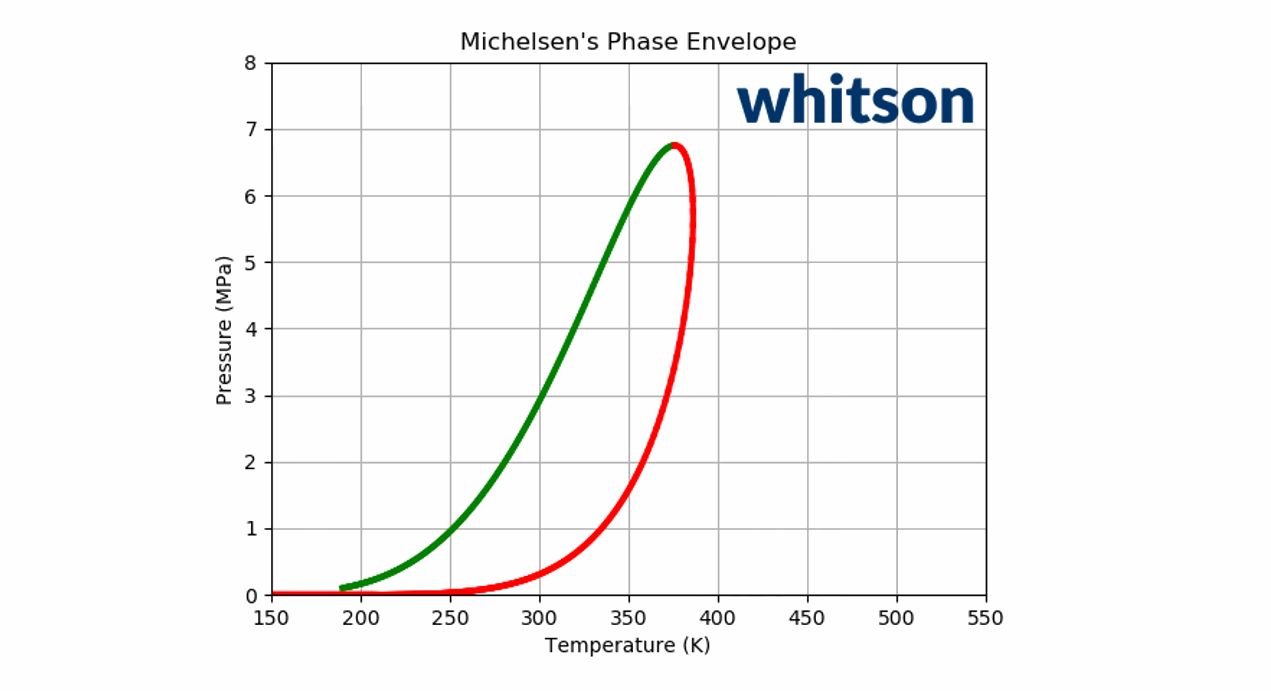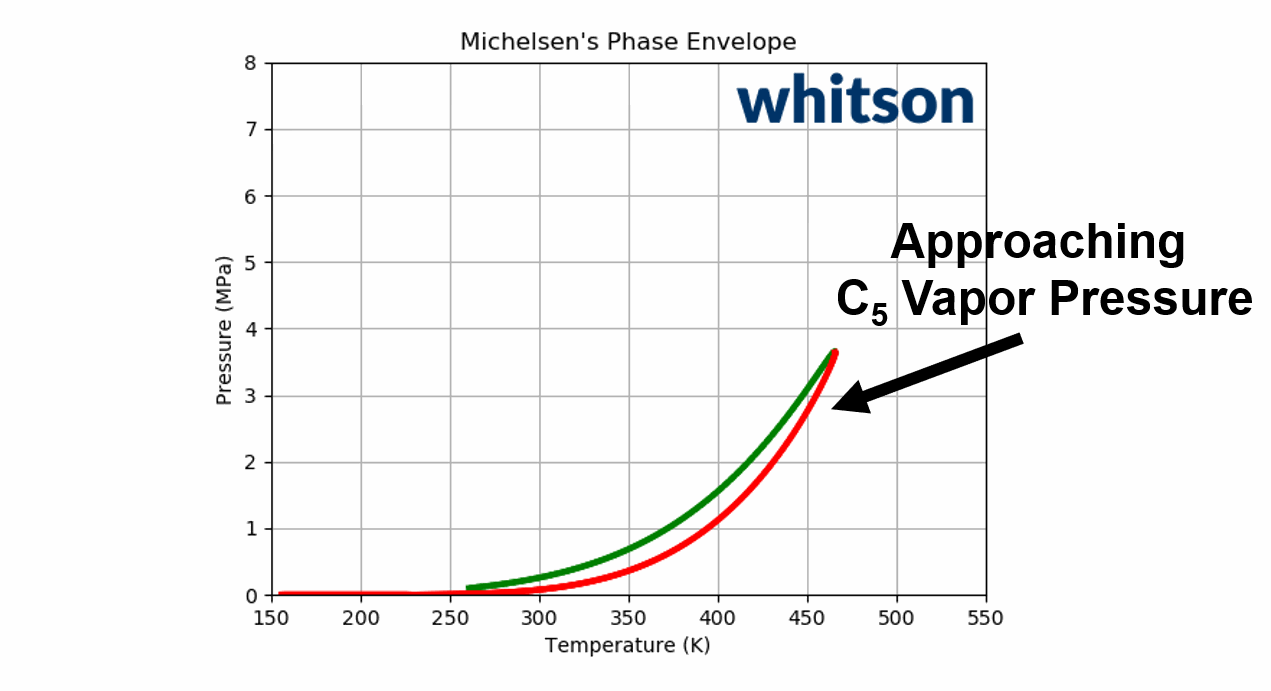
Animation 2: An animation of the phase envelope for a \(C_2\)-\(C_5\) binary system at all possible combinations of compositions going from ~100% \(C_5\) to ~100% \(C_2\).

Pseudo-Vapor Pressure

For a given mixture, the components have to be mixed to a single pseudo-component which is used in the EOS calculation. Similarly, a pseudo-vapor pressure can be calculated for this pseudo-component based on the mixture. For the system given in Figure 4, this pseudo-vapor pressure was calculated and is shown in Figure 5.

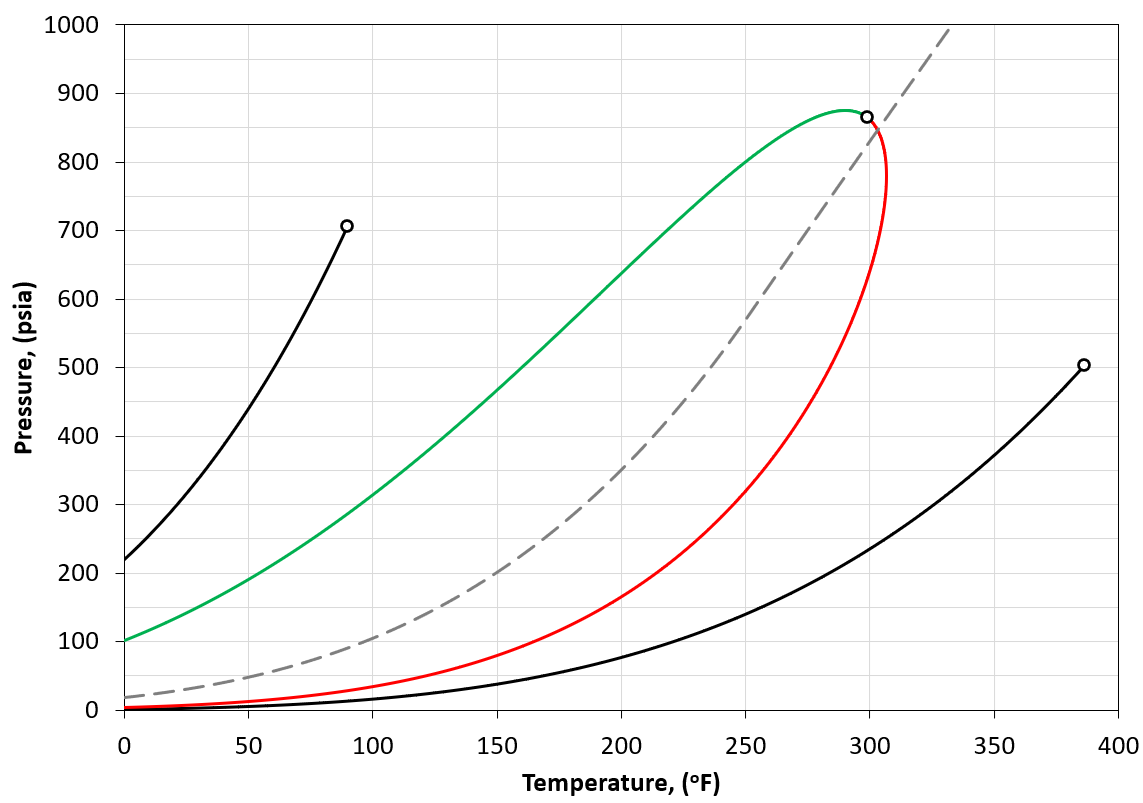
Figure 5: The same system as Figure 4, but with the associated pseudo vapor pressure curve for the mixture (grey dashed line).