Equilibrium Ratios
The equilibrium ratio (K-value), defined in equation \eqref{eq:def}, is one of the most important thermodynamic quantities for petroleum systems. The reason for this is the direct connection it has on the flash calculation, which is a key phase behavior calculation. Furthermore, the K-values have an intuitive and simple physical meaning. Given a K-value for a specific component at certain conditions, the magnitude will determine the affinity the component has to be in the vapor phase (K-value greater than 1) or the liquid phase (K-value smaller than 1). Theoretically, the K-values can be measured in the lab and an argument can be made that accurate K-value measurements is the best source of PVT data used in equation of state model development.
The shape of the K-value is typically divided into the low-pressure region and the high-pressure region. For the low pressure region the K-values tend to be inversely proportional to the pressure (\(K_i \propto 1/p\)) yielding a -1 slope on a log-log plot and is said to follow Raoult's law and Dalton’s law
where \(p_{vi}(T)\) is the vapor pressure of component \(i\). In the high-pressure region, all the K-values appear to converge to unity at the convergence pressure.
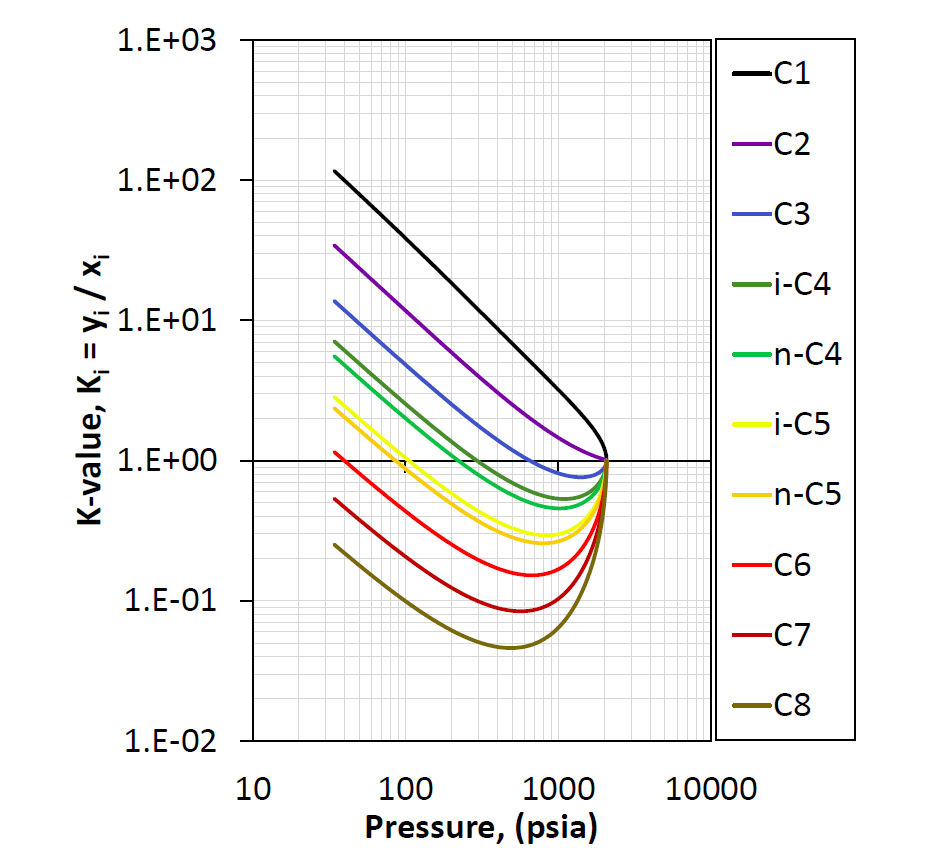
Figure 1: An example of pressure dependent K-values at a given temperature and composition.
Definition
The formal definition of the K-values are given by
Areas of Use
The main area of use for the K-value is, as mentioned above, that it is a key quantity in the isothermal flash calculation. The K-value is some sense the driving mechanism behind most PVT calculations. The shape of the K-values (especially for high-pressures) drives the phase behavior of the fluid. For this reason, the K-value consistency check is essential as part of the equation of state model development.
Correlations
A wide range of correlations have been developed to estimate the K-values for hydrocarbon systems. However, as noted above, the only sure way to determine the true K-value is to solve the flash routine. Below, some correlations are given for reference.
Hoffman Correlation
where
By re-arranging equation \eqref{eq:hoffman} and take the base-10 logarithm of both sides yield
such that \(A_0\) and \(A_1\) become the intercept and slope of a straight line on a log-log plot. This is the basis for the Hoffman quality check plot.
Wilson Correlation
Note that the Wilson correlation is identical to the Hoffman correlation for \(A_0=\log{(p_{sc})}\) and \(A_1=1\) in equation \eqref{eq:hoffman} and the Edmister correlation 1 is used for the acentric factor.
Modified Wilson Correlation
A modified version of the Wilson equation was proposed by Whitson and Torp in their 1981 paper 2.
where \(A_2\) is a constant sometimes used defined as 0.7, \(p_{ci}\) is the component critical pressure, \(p_k\) is the convergence pressure, \(\omega_i\) is the acentric factor, \(p_{ri}\) is the reduced pressure defined by \(p_r=p/p_c\) and \(T_{ri}\) is the reduced temperature defined by \(T_r=T/T_c\). The units for equation \eqref{eq:mod_wilson} and \eqref{eq:A1} are psia for the pressure and R in temperature.
Standing Correlation
The Standing correlation for K-values was developed using the Hoffman correlation and tuned for low pressure K-value data3. The specified conditions where the correlation applies was described to be at \(p<1000\)psia and \(T<200^\circ\)F. The Standing correlation is often used to estimate the K-values for separator processes, specifically for the Hoffman plot quality check used for separator samples.
The equation for the Standing correlation is given by
where
Unlike the Hoffman correlation, Standing gives an expression for \(A_0\) and \(A_1\) as a function of pressure. The correlation also gives a method for calculating \(b_i\) and \(T_{bi}\) for \(C_{7+}\) based on the pressure and temperature.
In the Standing correlation given above, the units for pressure are in psia and the temperature is given in R.
Standing also gives a list of the component values for \(b_i\) and \(T_{bi}\) and they are given in the table below.
| Component | \(b_i\)(cycle-\(^\circ\)R) | \(T_{bi}\) (\(^\circ\)R) |
|---|---|---|
| N\(_2\) | 470 | 109 |
| CO\(_2\) | 652 | 194 |
| H\(_2\)S | 1136 | 331 |
| C\(_1\) | 300 | 94 |
| C\(_2\) | 1145 | 303 |
| C\(_3\) | 1799 | 416 |
| i-C\(_4\) | 2037 | 471 |
| n-C\(_4\) | 2153 | 491 |
| i-C\(_5\) | 2368 | 542 |
| n-C\(_5\) | 2480 | 557 |
| C\(_6\) | 2738 | 610 |
Simplified Flash
In 1986 Michelsen introduced a new approach to solve the flash in a simplified manner for an EOS model where all the BIPs were set to zero4. This simplified flash approach allows for a direct calculation of the K-values from the EOS parameters. The solution to Michelsen's procedure is given by
where \(b_i\) is the component EOS parameter and
where \(u_i\) can be the vapor molar amount (\(y_i\)) or liquid molar amount (\(x_i\)).
By using the fact that \(K_i = \phi_i^L/\phi_i^V\) and taking the natural logarithm of both sides yields
which can be calculated from equation \eqref{eq:simp_flash_coef}.
-
W. C. Edminster. Applied hydrocarbon thermodynamics, part 4: compressibility factors and equations of state. 1958. ↩
-
C. H. Whitson and S. B. Torp. Evaluating constant volume depletion data. In SPE Annual Technical Conference and Exhibition, paper SPE–10067–MS. Society of Petroleum Engineers, 1981. doi:https://doi.org/10.2118/10067-MS. ↩
-
M.B. Standing. A set of equations for computing equilibrium ratios of a crude oil/natural gas system at pressures below 1,000 psia. Journal of Petroleum Technology, 31:paper SPE–7903–PA, 1979. doi:https://doi.org/10.2118/7903-PA. ↩
-
M. L. Michelsen. Simplified flash calculations for cubic equations of state. Industrial & Engineering Chemistry Process Design and Development, 25:184–188, 1986. ↩